吳子青: Radial Basis Function ANN 輻狀基底類神經網路

Radial Basis Function ANN 輻狀基底類神經網路

前言：
利用RBF ANN 作簡短的介紹類神經網路的原理，並以老師上課的例子以類神經網路作簡單的應用，在這裡利用ANN 作 “ 函數模擬 ” 。

類神經網路介紹：
類神經網路（Artificial Neural Networks, ANNs）或譯為人工神經網路，其主要的基本概念是嘗試著模仿人類的神經系統。

它是由很多非線性的運算單元（即：神經元 neuron）和位於這些運算單元間的眾多連結（links）所組成，而這些運算單元通常是以平行且分散的方式來進行運算以電腦的軟硬體來模擬生物神經網路的資訊處理系統。

整個ANN的聚集形式就如同人類的大腦一般，可透過樣本或資料的訓練來展現出學習（learn）、回想（recall）、歸納推演（generalize）的能力。

類神經網路在處理複雜的工作時
(1)不需要針對問題定義複雜的數學模式，
(2)不用去解任何微分方程、積分方程或其他的數學方程式，
(3)藉由學習來面對複雜的問題與不確定性的環境。

輻狀基底函數類神經網路介紹(RBF ANN)
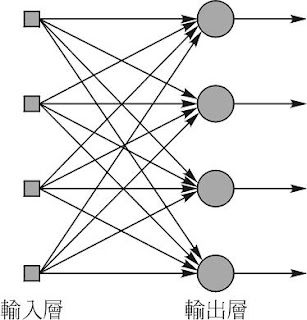
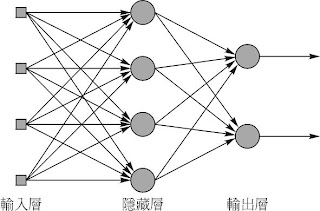
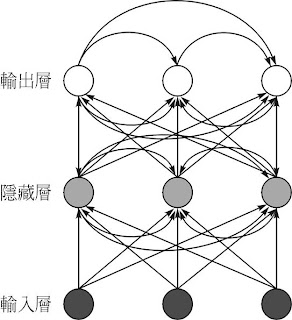
或稱為半徑式類神經網路，特質主要在於摩擬大腦皮質軸突的局部調整功能
為基本前饋式類神經網路
其可視為在解決高維度空間的曲線調適問題

RBFANN 架構

RBFANN演算流程
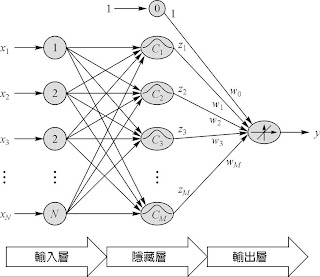
1. 處理資料 (輸入項與目標輸出項)
2. 決定類神經網路架構
3. 決定初始中心點位置 (類神經元)
4. 利用RBFANN學習演算法修正(1)中心點位置 (2)連結權重 (3)福狀基底半徑
5. 驗證與測試階段


程式流程
Step 1 :
想要利用RBF ANN模擬 matlab裡面z=peaks(X,Y)的函數
z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...
- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...
- 1/3*exp(-(x+1).^2 - y.^2)
可以看出 Peaks(X,Y) 這是一個非線性的方程式
正好用來測試類神經網路處理非線性的能力
取X,Y都介於-2和2間距0.2 共產生400筆資料各包含(X,Y, f(X,Y ))

Step 2
架構RBFANN 這裡選取輸入維度2, 中心點個數 100
以高斯函數為輻狀基底函數 演算次數 200次 學習速率0.01

Step3
將400筆資料依序丟入網路中進行訓練，並修正中心點位置 連結權重 福狀基底半徑 等資訊

Step4
製作演算流程動畫, 以3D圖上的黑點表示 input data , 以mesh 網格表示ANN模擬函數的結果, 若資料點和mesh網格重合則表示模擬效果優良

Step 5
達到停止條件或最大演算步數則停止, 結果為rmse 越小表示越好

Step 6
製作GUI介面

程式內容
clear all;
iter=100;
nc=100;
goal=0.01;
lr_w=0.01;
lr_c=0.01;
lr_s=0.01;

% p 為輸入資料點，N×K矩陣，N是輸入資料維度，K是資料點數
% t 為目標輸出值，1×K矩陣
% newcenter已選定的中心點，N×nc矩陣
% iter為指定演算代數
% goal為指定之網路誤差
% lr_w為調整權重之學習速率
% lr_c為調整中心點之學習速率
% lr_s為調整標準偏差? (sigma)之學習速率
% W為輸出層權重，nc×1矩陣
% yh為網路輸出值，1×K矩陣
% rmse為目標輸出值與網路輸出值之RMSE

%輸入函數
[X,Y] = meshgrid(-2:0.2:2);
Z = 3*peaks(X,Y);

[mm,nn]=size(Z);
PA=zeros(3,mm*nn);
for i=1:mm
for j=1:nn
PA(1,(i-1)*nn+j)=X(i,j);
PA(2,(i-1)*nn+j)=Y(i,j);
PA(3,(i-1)*nn+j)=Z(i,j);
end
end
clear i j ;

p=PA(1:2,:);
t=PA(3,:);

[nd,np]=size(p);
k=randperm(np);
newcenter=p(:,k(1:nc));

clear nd np nc k ;

nc=size(newcenter,2);
[nd,np]=size(p);
phii=zeros(1,nc);
Dic=[];
phi=[];
itimetemp=1;
for i=1:nc
for j=1:nc
Dic(j,i)=norm(newcenter(:,i)-newcenter(:,j));%計算center的距離
end
end
sigma=(max(max(Dic))/sqrt(nc));%計算基底函數的標準偏差σ(sigma)
for i=1:nc
for j=1:np
phi(j,i)=exp(-(norm(newcenter(:,i)-p(:,j))/sigma)^2);%計算center與input各點的距離
end
end

W=pinv(phi)*t';%初始權重W
newsigma=sigma*ones(nc,1);
for itime=1:iter
for j=1:np
for i=1:nc
Dip(i)=norm(p(:,j)-newcenter(:,i));%計算center與input各點的距離
phii(i)=exp((-1/(newsigma(i)^2))*(Dip(i)^2));
end
if(itime==iter)
finalphii(j,:)=phii;
end
yh(j)=phii*W;
e(j)=yh(j)-t(j);
for k=1:nc
newcenter(:,k)=newcenter(:,k)-lr_c*(e(j)*W(k)/(newsigma(k)^2))*phii(k)*(p(:,j)-newcenter(:,k));%更新基底函數的中心值c
newsigma(k)=newsigma(k)-lr_s*(e(j)*W(k)/(newsigma(k)^3))*...
phii(k)*(norm(p(:,j)-newcenter(:,k)))^2;%更新基底函數的標準偏差σ
end
W=W-lr_w*e(j)*phii';%更新權重向量W
end
err1=sqrt(mse(yh-t));
err2(itime)=mse(yh-t);
if(itime/100-itimetemp==0)
itimetemp=itimetemp+1;
itime
end
if(err1<=goal)
break;
end

for i=1:np
for m=1:nc
phii(m)=exp(-(norm(p(:,i)-newcenter(:,m))/newsigma(m))^2);
end
yh(i)=phii*W;
end
for i=1:mm
for j=1:nn
ZZ(i,j)=yh((i-1)*nn+j);
end
end
rmse=sqrt(mse(yh-t));
clear yh;
%figure1
figure(1)
plot3(PA(1,:),PA(2,:),PA(3,:),'.','markersize',5);
grid on
hold on
mesh(X,Y,ZZ);
hold off
M(itime)=getframe;
RMSE(itime)=rmse;
end %time end
movie(M,1,2);

figure(2)
plot(RMSE);
title('rmse value');
xlabel('epoch step');
ylabel('rmse')
clear Dic Dip W ans e err1 err2 finalphii goal itime itimetemp;
clear j k lr_c lr_s lr_w m nc nd newsigma np p phi phii sigma itime m n mm nn;
clear PA X Y Z ZZ newcenter;
clear itre i M iter t RMSE;